When trying to use glmnet, probably the most popular R package for regularized regression, to do weighted lasso estimation, I struggled a lot on penalty.factor in the glmnet() function. After doing a series of experiments, I finally understood how it would work and how it affects the lambda sequence. Hope this article can help clarify your confusion as well.
Background Knowledge
Firstly, let me introduce some background knowledge. The main goal of penalty.factor is to allow different shrinkage on different betas and hence it can be used to perform weighted lasso. And a lambda sequence is used to get the solution path of the regularized problem. As shown below is the formula of the optimization objective when penalty.factor is specified.

The default value for penalty.factor is rep(1, nvars) and the official documentation for this argument in the glmnet() function:
Separate penalty factors can be applied to each coefficient. This is a number that multiplies
lambdato allow differential shrinkage. Can be 0 for some variables, which implies no shrinkage, and that variable is always included in the model. Default is 1 for all variables. Note: the penalty factors are internally rescaled to sum to nvars, and the lambda sequence will reflect this change.
My confusion was mainly caused by the bolded sentence as I didn’t know how the lambda sequence would change accordingly. And not knowing the change would prevent me from assigning correct values to the lambda argument. Therefore, I performed a series of experiments to check it.
Findings
- If the lambda sequence is specified by the user, instead of the default one generated by the function, then no matter how we scale the penalty.factor, the lambda sequence remains the same, just the one provided by the user.
- If, however, the user doesn’t provide any lambda sequence, then the function will automatically generate a lambda sequence as the default. In this case, if we uniformly scale the penalty.factor, then the lambda sequence will not change, as the penalty.factor will be rescaled internally. While if the scaling is not uniform, then the lambda sequence will change, not just values, but also the length of the vector in some cases.
Experiments in R
Let us do some experiments to validate the above findings.
> ###===== When using the default lambda sequence ======###
> x <- matrix(rnorm(100 * 20), 100, 20)
> y <- rnorm(100)
>
> fit <- glmnet(x, y)
> l1 <- fit$lambda
>
> # default value
> penalty.factor <- rep(1, ncol(x))
> fit2 <- glmnet(x, y, penalty.factor = penalty.factor)
> l2 <- fit2$lambda
>
> # uniformly scale
> penalty.factor <- rep(2, ncol(x))
> fit3 <- glmnet(x, y, penalty.factor = penalty.factor)
> l3 <- fit3$lambda
>
> # not uniformly scale
> penalty.factor <- c(rep(1, ncol(x)/2), rep(2, ncol(x)/2))
> fit4 <- glmnet(x, y, penalty.factor = penalty.factor)
> l4 <- fit4$lambda
>
> # if 0 then mean all entries are equal
> sum(l1!=l2)
[1] 0
> sum(l1!=l3)
[1] 0
> sum(l1!=l4)
[1] 72
Warning message:
In l1 != l4 :
longer object length is not a multiple of shorter object length
> ###===== When using the user-specified lambda sequence =====###
> # specify a self-defined lambda sequence
> lambda.seq <- exp(-seq(0.01, 1, length.out = 30)) / 10
>
> fit1 <- glmnet(x, y, lambda = lambda.seq)
> l1 <- fit1$lambda
>
> penalty.factor <- rep(1, ncol(x))
> fit2 <- glmnet(x, y, penalty.factor = penalty.factor, lambda = lambda.seq)
> l2 <- fit2$lambda
>
> penalty.factor <- rep(2, ncol(x))
> fit3 <- glmnet(x, y, penalty.factor = penalty.factor, lambda = lambda.seq)
> l3 <- fit3$lambda
>
> penalty.factor <- c(rep(1, ncol(x)/2), rep(2, ncol(x)/2))
> fit4 <- glmnet(x, y, penalty.factor = penalty.factor, lambda = lambda.seq)
> l4 <- fit4$lambda
>
> penalty.factor <- c(rep(2, ncol(x)/2), rep(4, ncol(x)/2))
> fit5 <- glmnet(x, y, penalty.factor = penalty.factor, lambda = lambda.seq)
> l5 <- fit5$lambda
>
> sum(l1!=l2)
[1] 0
> sum(l1!=l3)
[1] 0
> sum(l1!=l4)
[1] 0
> sum(l1!=l5)
[1] 0
Internal Rescaling in Weighted Lasso
One critical point to keep in mind is that, due to rescaling, you need to think twice about the lambda argument when you specify it yourself. It is likely to perform a lasso solving procedure that doesn’t conform to the desired objective function once you slip you mind.
To illustrate this, let’s go back to my original problem, solving a weighted lasso problem. My problem comes from Shen et al. 2012 paper on glmtlp, where the unconstrained dual problem can be reduced to a general weighted lasso problem:

We use the indicator function as the penalty.factor, and we can see that for different iterations, the penalty.factor will differ. Therefore, the scale is not uniform. But the good news is: from the above investigation, we already know that if the lambda sequence is provided by the user, then penalty.factor will not affect the lambda sequence. So we have full a control on the lambda sequence. What remains is to do proper adjustment on the lambda sequence.
- lambda.wt doesn’t sum up to nvars, so it will be internally rescaled to
lambda.wt / sum(lambda.wt) * sum(penalty.factor)implicitly. Namely, c_j now is actually the following.

- To get the desired objective, we then need to rescale lambda accordingly.
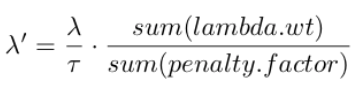
Then for each iteration, we can write the code as follows. (Modified from the glmtlp R package code. The code in CRAN might have missed the division by tau part in my opinion.)
penalty.factor <- rep(1, nvars) # default
lambda.wt <- (abs(b0)<=tau)
if (length(lambda.wt[abs(lambda.wt)<eps0])>nvars/2)
lambda.wt[abs(lambda.wt)<eps0] <- eps0lambda.wt <- lambda.wt * penalty.factor
lambda.tmp <- lambda[k] * (sum(lambda.wt) / sum(penalty.factor)) / taures <- glmnet(x, y, family=family, weights = weights, offset=offset, lambda=lambda.tmp, penalty.factor=lambda.wt, standardize = standardize, intercept = intercept,lower.limits = lower.limits, upper.limits = upper.limits, standardize.response = standardize.response)
Cool! We are done! Hope this article helps give you a better sense of how penalty.factor work in the glmnet package. Further discussions are welcome.
References
- Shen, Xiaotong, Wei Pan, and Yunzhang Zhu. “Likelihood-based selection and sharp parameter estimation.” Journal of the American Statistical Association 107.497 (2012): 223–232.APA
- glmTLP source code on Github: https://github.com/cran/glmtlp/blob/master/R/glmTLP.R.
- A deep dive into glmnet: penalty.factor